![]()
3-й час. Арифметические действия в Python
- Сложение и вычитание
- Умножение, отношение и деление по модулю
- Округление, функции floor() и ceil()
- Возведение в степень
- Применение скобок
- Некоторые нюансы и секреты
- Резюме
- Практикум
3-й час
Арифметические действия в Python
В этой главе мы изучим основные арифметические действия, которые можно выполнять в Python и IDLE. Хотя они, по сути, предельно простые, но на их основе строятся все сложные математические вычисления, некоторые из которых мы рассмотрим далее в этой книге. Впрочем, чтобы стать хорошим программистом, совершенно необязательно быть доктором математических наук. В большинстве случаев от Вас потребуются лишь знания основ математики на уровне средней школы. Если же Вам приходилось изучать курс высшей математики, значит, Вы подготовлены на все 100%. Так что не бойтесь, смело вперед. Уж, по крайней мере, в этой главе с математикой у Вас проблем не будет, только с программированием.
Тем, кто не слишком преуспевал в математике, не следует отчаиваться. В старших классах средней школы я, как и все, изучал алгебру и почти провалил её на экзамене (у меня был откровенно слабый преподаватель, но что ещё хуже, я не уделял этому предмету должного внимания). Много позже, на армейском вводном курсе по электронике я наверстал упущенное и усвоил некоторые из основных методов. Через два года после окончания этого курса я стал его преподавать.
В любой начальной школе ещё с первого класса изучают операции сложения и вычитания, так как это тот столп, на котором держится вся математика. Я не сомневаюсь, что Вы знаете, как выполнять эти действия. И что особенно приятно, в Python (как, впрочем, и в любом другом языке программирования) все происходит именно так, как Вы и предполагаете.
Выполним несколько упражнений с операциями сложения и вычитания. Запустите интерпретатор Python, введя python в приглашении командной строки, а затем в приглашении Python введите 1 + 1. Если после нажатия клавиши <Enter> Python не ответит Вам результатом 2, значит, у Вас большие проблемы! Теперь попробуйте выполнить более сложные задачи, например сложите нескольких больших чисел, а затем сложите положительные и отрицательные числа. При манипуляциях с числами Вам поможет следующая графическая схема. Представьте себе все целые числа в виде точек, расположенных на бесконечной линии с нулем посередине. Тогда, путешествуя вперед или назад с помощью операций сложения и вычитания, Вы можете перейти к любому числу. Например, предположим, что Вы находитесь в позиции 0 и хотите попасть в позицию -45. Очевидно, что для этого Вы должны пропутешествовать назад на 45 точек. Но добраться туда можно двумя способами: можно прибавить отрицательное число или вычесть положительное. Попробуйте проверить оба метода. В окне интерпретатора Вы должны получить результаты, показанные на рис. 3.1.

Рис. 3.1. 1 + 1
Вам уже стало скучно от примитивности примеров? Давайте теперь попробуем складывать и вычитать действительно большие числа. Выполнение этой задачи с помощью карандаша и бумаги, безусловно, не вызовет у Вас никаких проблем. Даже если это будут очень-очень большие числа, просто немного терпения, и в результате обязательно получится правильный ответ. Но если Вы привыкли пользоваться современным калькулятором или раритетными в наши дни счетами, то проблема может возникнуть из-за того, что ваши числа превысят максимально допустимую разрядность Вашего электронного или деревянного инструмента.
Не сложно определить максимально допустимое число для калькулятора или счёт. Просто пересчитайте число значимых ячеек на табло или число прутиков в раме счёт. При использовании компьютера предельность вычислений не столь очевидна. Дело в том, что между внутренним представлением чисел, как его видит компьютер, и тем форматом, в котором число отображается на экране, существуют большие различия. Для внутреннего представления чисел большинство компьютеров использует 32 бита, причём один из этих битов обычно используется для представления знака числа, указывающего, является ли данное число положительным или отрицательным. Поэтому для собственно числового значения остаётся всего только 31 бит. Таким образом, в Python самым большим допустимым целым знаковым числом является значение 2 147 483 647 (два миллиарда с мелочью).
*Прим. В. Шипкова: на конец 2005 г. в продаже по вполне доступным ценам имеются машины с 64-битами. И на самом деле 2^32 - это не предел для Питона, расстраиваться не надо. Об этом речь пойдёт дальше.
Конечно, Вы уже слышали термин бит прежде, но давайте ещё раз рассмотрим, что он означает, хотя бы для того, чтобы прибавить Вам уверенности. Бит — это одноразрядное значение типа "да-нет", "включено-выключено" или в числовом выражении — 0 или 1. И больше ничего иного. Чтобы представлять большие числа, необходимо объединить вместе несколько таких битов. Это как раз то, чем занимаются современные компьютеры. Они объединяют вместе свои биты в байты (8 битов) и слова (как правило, 32 бита), из которых затем и складывается весь машинный код.
*Прим. В. Шипкова: физически значение "да-нет" кодируется наличием или отсутствием напряжения, по значению близкое к напряжению питания. Как правило 1,5...1,7 Вольта для процессора и 3,1...3,5 Вольта для оперативной памяти (сейчас могут использоваться ещё меньшие напряжения).
На рис. 3.2 показано, что произойдет, если попытаться ввести числа, приближающиеся к этой 32-битовой границе. На показанных примерах видно, что наиболее эффективный метод использования всех 32 битов, отведённых для представления целого числа, состоит в переходе к шестнадцатеричному формату. Обусловлено это тем, что числа в шестнадцатеричном формате обрабатываются компьютером как беззнаковые, поэтому могут быть использованы все биты.
В Python есть специальное имя для самого большого знакового значения: maxint. Эта константа опредёлена в специальном модуле под названием sys. Чтобы иметь возможность обращаться к maxint из своих программ, необходимо импортировать модуль sys. Позже Вы узнаете о том, как выполняется импортирование. Пока просто примем, что если нужен программный блок, содержащийся в каком-либо модуле, то вместо того чтобы переписывать этот блок в своей программе, его можно импортировать из имеющегося модуля.
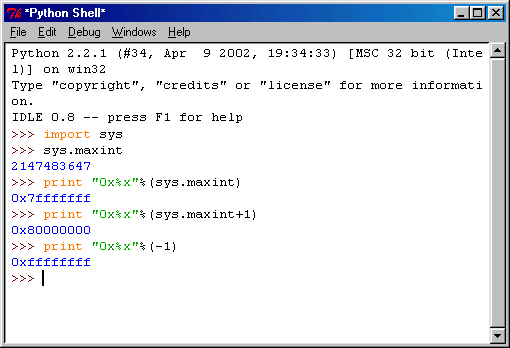
Рис. 3.2. 32-разрядные числа
Шестнадцатеричный формат является одним из способов визуализации двоичных чисел в понятном для человека виде. Двоичные числа проще преобразовывать в шестнадцатеричные, чем в десятеричные. Любое 4-рязрядное двоичное число можно представить одноразрядным шестнадцатеричным. Так, двоичному числу 1111b будет соответствовать шестнадцатеричное число Fh.
*Прим. В. Шипкова: все двоичные числа принято в конце отмечать буквой "b" - binary, а шестнадцатеричные буквой "h" - hex, или hexadecimal(игра слов: hex - "ведьма").
Под термином шестнадцатеричное подразумевается представление числа по основанию 16. Это означает, что ряд шестнадцатеричных цифр следует от О до F, т.е. 0-15 в десятичном представлении. Если Вы хотите произвести впечатление на своих друзей и выглядеть суперкрутым компьютерным специалистом, пронумеруйте кассеты своей коллекции видеофильмов в шестнадцатеричном формате, начиная с кассеты под номером 0.
Отлично, теперь давайте посмотрим, как отреагирует Python, если в математическом действии использовать число, превышающее допустимый предел. Например, давайте прибавим к единице число 9 999 999 999. На рис. 3.3 показано, что в ответ на это скажет Python.

Рис. 3.3. Число слишком большое, чтобы Python смог его проглотить
Мда-а... Что бы это значило? Именно то, что говорится в сообщении об ошибке: число, которое мы прибавили, оказалось слишком большим для Python, чтобы он мог правильно его обработать. Другими словами, Python попытался преобразовать число 9 999 999 999 в двоичный формат, но для этого ему не хватило битов. Мы получим аналогичный результат, если попытаемся отнять большое число. Так что же остаётся делать? Оказывается, существует очень простой метод обойти это ограничение: необходимо всего лишь сообщить Python, что он должен обрабатывать большое число именно как большое число. Для этого мы даем Python подсказку — всего лишь добавляем символ L в конце любого большого числа, если полагаем, что оно может вызвать переполнение буфера (именно это подразумевается под нехваткой битов). На рис. 3.4 показан пример такого решения.

Рис. 3.4. Снова прибавляем большое число
Добавление символа L после любого большого числа сообщает Python, что это длинное число. Длинные числа могут быть сколь угодно большими. Число разрядов ограничено только объемом памяти Вашего компьютера и вашим терпением. Теперь давайте поработаем с действительно большими числами. Введите следующее число в основное окно программы IDLE (можете выгрузить из Internet текстовый файл ftp://www.pauahtun.org/pub/googol.txt, в котором содержится это число, или просто введите единицу, а за ней 100 нулей):
1000000000000000000000000000000000000000000000000000000000000000000
0000000000000000000000000000000000000L
Добавьте после этого числа знак "плюс" (+), а затем снова вставьте точно такое же число и нажмите клавишу <Enter>. Результат показан на рис. 3.5.

Рис. 3.5. Сложение двух длинных чисел
Число, состоящее из единицы с сотней нулей, называется гугол (googol). Это название было введено в обиход американским математиком Эдвардом Каснфом (Edward Kasner), a придумано его девятилетним племянником, Милтоном Сироттой (Milton Sirotta).
Вы можете складывать обычные целые числа и длинные целые числа без каких бы то ни было проблем. Правилами Python устанавливается, что всякий раз, когда Вы выполняете арифметические функции с любыми двумя операндами, меньший операнд приводится к типу большего. Таким образом, если Вы суммируете 1 + 100000000000000000000000L, Python автоматически преобразует 1 в 1L.
Математические операторы, например суммирования (+) и вычитания (-), оперируют с операндами. Например, выражение "1 + 4" обозначает: "применить оператор суммирования к операндам 1 и 4".
Вам придётся также столкнуться ещё с третьим типом чисел — числа с плавающей запятой. Это числа, в которых есть десятичная запятая, например 1,1 и 3,14159265359. (В англоязычных странах для представления десятичных чисел вместо плавающей запятой используется точка(!!!). Обратите на это внимание и не удивляйтесь, что когда в тексте мы говорим о плавающей запятой, то в примерах ставим точку. Примечание: использование запятой в коде программы Python вызовет ошибку.) Иногда в результате сложения и вычитания таких чисел выводится результат, который Вы даже и не предполагали получить. Так, к примеру, на рис. 3.6 показано выражение, результатом которого Вы, скорее всего, ожидали бы увидеть 0,00001.

Рис. 3.6. Вычитание чисел с плавающей запятой
В общем-то, Вы такой результат и получили. Не удивляйтесь, просто число представлено в экспоненциальном формате, о котором мы поговорим более подробно в последнем разделе этой главы. А пока перейдем к следующей теме.
Умножение, отношение и деление по модулю
В предыдущем разделе Вы узнали о сложении и вычитании обычных целых чисел, длинных целых чисел и чисел с плавающей запятой. В данном разделе Вы познакомитесь с умножением, делением и с кое-чем таким, о чем Вы могли ещё не слышать, — делением по модулю. При этом будут использоваться те же типы чисел.
И снова позволю себе повториться — правила выполнения этих операций в Python не очень отличаются от тех, которые Вам знакомы со школы. Единственный нюанс, который необходимо всегда учитывать, состоит в том, что тип операнда в значительной степени определяет то, как Python будет обрабатывать числа. Например, деление числа 10 на 4,0, как показано на рис. 3.7, даёт ожидаемый результат — 2,5.

Рис. 3.7. Деление чисел
Но в случае, показанном на рис. 3.8, мы получаем совершенно иной ответ.

Рис. 3.8. ещё один пример деления
Несовпадение ответов объясняется тем, что в первом случае, указав десятичную запятую (точку) в операнде 4.0, мы сообщили Python, что нам небезразлична информация об остатке деления после десятичной запятой. Во втором случае, опустив десятичную запятую, мы явно указали Python, что нас интересует только целая часть числа. И Python любезно отбросил дробную часть числа (.5), о которой мы сообщили ему, что в ней не нуждаемся. Таким образом, как и в случае с операциями сложения и вычитания, Python определяет формат результата по форматам переданных ему операндов. Поэтому Вам следует внимательно относиться к типам операндов. Очень просто потерять десятичную запятую там, где в действительности Вы ожидаёте её увидеть. Такая потеря в дальнейшем может привести к неправильной работе программы.
Та лёгкость, с которой при делении можно получить неожиданный или даже неправильный результат, была и остаётся темой жарких дебатов, ведущихся и по сей день среди участников телеконференций по тематике программирования на Python. Некоторые респонденты доказывают необходимость применения специального оператора, отличного от обычного оператора деления (/), который бы указывал Python, что требуется выполнить целочисленное деление (как показано на рис. 3.8), или наоборот, устанавливающего для результата формат числа с плавающей запятой (рис. 3.7). Так, в качестве специальных операторов деления предлагалось использовать сочетание символов /. для деления только с плавающей запятой и сочетание // — только для целочисленного деления. Но эти предложения не нашли поддержки у Гуидо, хотя он обещал подумать над этим вопросом и внести некоторые изменения в будущие версии Python.
*Прим. В. Шипкова: я не поленился проверить верно ли для версии 2.4.1 деление с "бек слешем" - обратной косой чертой. Но увы, воз и ныне там. А надо бы.
Как и в случаях со сложением и с вычитанием, длинные целые числа можно использовать в выражениях умножения и деления (рис. 3.9).
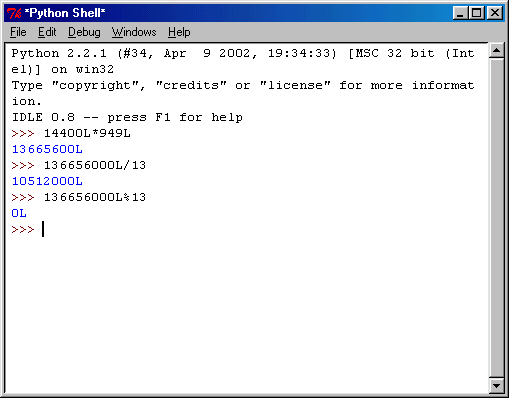
Рис. 3.9. Деление и умножение длинных чисел
Обратите внимание, что в третьем примере, показанном на рис. 3.9, используется новый оператор, обозначенный символом % — деление по модулю. С помощью этого оператора можно осуществлять деление обычных или длинных целых чисел, причём от полученного результата отбрасывается целая часть числа (частное), а остаток возвращается. Например, выражение 136656000L % 13 возвратит нуль, потому что число 136 656 000 делится на 13 без остатка. Деление по модулю — очень удобное средство, например при вычислении календарных дат. Вот один из примеров. Практически во всех календарях присутствует високосный год, который можно вычислить делением по модулю. А в тех календарях, где високосные годы отсутствуют, ситуация настолько сложна, что без деления по модулю вообще не обойтись. Примером последнего может быть календарь Майя. С нашим григорианским календарем ситуация попроще, так как високосные годы в нём присутствуют. В юлианском календаре, от которого собственно и произошел григорианский, действует очень простое правило високосного года: любой год, значение которого делится без остатка на 4, является високосным. Правило григорианского календаря вносит поправку в эту формулировку, утверждая, что годы столетий (1700, 1900 и т.д.) являются високосными только в том случае, если они делятся без остатка на 400. На рис. 3.10 показано, как определить, является ли 2000-й год високосным.
Рис. 3.10. Определение високосного года
Год 2000 — високосный, а 1900 — нет. Я как-то читал один детектив, в котором следователь разбил "железное" алиби подозреваемого после того, как сообразил, что 1900-й год не был високосным. Я уже не помню в деталях ни саму историю, ни её автора, но факт остаётся фактом — иногда бывает важно быстро определить, является ли указанный год високосным.
Существует специальная функция, которую можно использовать для возвращения частного и остатка от деления. Функция divmod(x,y) возвращает результаты выполнения двух действий: х/у и х%у. Вы можете проверить это, введя в окне IDLE команду print divmod (53,13). Пара результатов будет показана в виде (4,1). В Python всегда возвращаются группы результатов, о чем мы поговорим позже.
Округление, функции floor() и ceil()
В этом разделе мы будем иметь дело исключительно с числами в формате с плавающей запятой. Во всех случаях, когда необходимо выполнить любую математическую операцию над числами с плавающей запятой, следует помнить об ограничениях, связанных с базовым представлением этих чисел компьютером. Компьютеры оперируют с числами только в двоичном формате, т.е. с основанием 2. В числах с основанием 2 присутствуют только две цифры — 0 и 1. Это идеальная система счисления для компьютеров, поскольку значения 0 и 1 могут быть представлены простым двух-позиционным переключателем. Электролампочка, тумблер, электросхемы на лампах или транзисторах — все это примеры двухпозиционных переключателей. Преобразование целых чисел, представленных на базе одной основы, к формату с другой основой является относительно простой процедурой, которой занимаются компьютеры и неплохо справляются с момента их появления. При смене основания числа не теряется ни "капли" информации. Всегда можно преобразовать числа к другой основе без какого-либо округления. Например, десятичному числу 15 точно соответствует шестнадцатеричное число F, и любое другое десятеричное число однозначно соответствует опредёленному шестнадцатеричному, восьмеричному, двоичному и т.д. В таком случае говорят, что при преобразовании целых чисел потери точности не происходит.
Но это утверждение справедливо только для целых чисел. Все меняется, стоит только вставить в число десятичную запятую. Способы, с помощью которых в компьютерах осуществлялось представление чисел с плавающей запятой, исторически были разнообразными, сложными и довольно противоречивыми. Только в течение последних нескольких лет появилось что-то похожее на стандарт представления чисел этого типа. Тем не менее многие полагают, что даже этот стандарт, IEEE-64, полон ловушек и недостатков. К сожалению, чтобы полностью раскрыть эту увлекательную тему, понадобится написать отдельную книгу не меньшего объема, чем данная. Но вряд ли такая книга выйдет, так как найдется не много людей, которые проявили бы к ней интерес. Уж больно это специфический вопрос для узкого круга специалистов. Пока вполне достаточно будет сообщить Вам, что проблем в этом вопросе множество, а их решение сопряжено со значительными трудностями.
На данном этапе Вам достаточно знать, что при работе с числами с плавающей запятой возникают проблемы, связанные с потерей точности. Причем довольно неожиданным оказывается тот факт, что умножение и деление при таких обстоятельствах сопровождается определённой погрешностью, которая умеренно возрастает при повторных операциях, тогда как повторное сложение и вычитание существенно увеличивают погрешность. Из этого следует мораль — необходимо с осторожностью и умеренностью использовать сложение и вычитание чисел с плавающей запятой, а из двух способов решения задачи выбирать тот, где умножение и деление превалируют над суммированием и вычитанием.
Когда появляется необходимость выполнять математические действия с числами с плавающей запятой, рано или поздно возникает потребность преобразовать некоторые результаты, представленные в формате числа с плавающей запятой, в целые числа или в длинные целые числа. Для выполнения этой задачи в Python имеется простой способ, который состоит в том, чтобы использовать встроенные функции преобразования типов. Несколько примеров их применения показаны на рис. 3.11.
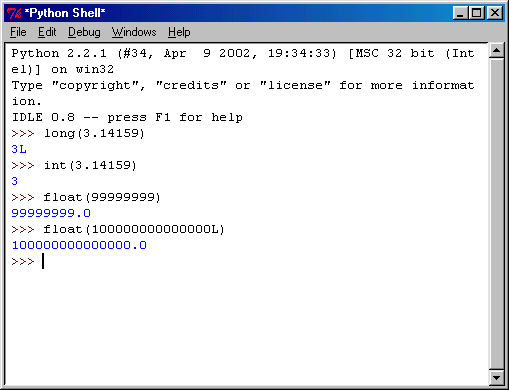
Рис. 3.11. Несколько примеров преобразования типов
Преобразования типов часто сопровождаются округлением значения. Иногда требуется округлить результат к большему значению, иногда — к меньшему. Для этого существуют специальные методы округления, позволяющие контролировать данную операцию: floor() и ceil(). Помните, как раньше мы уже импортировали модуль sys? Точно так же всякий раз, когда Вам понадобится использовать математические функции, следует импортировать модуль math. Но теперь мы воспользуемся другой инструкцией импортирования модулей (рис. 3.12).
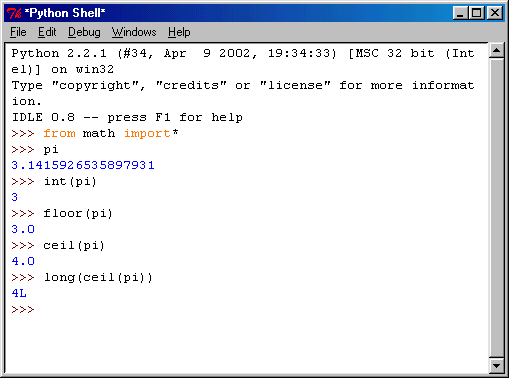
Рис. 3.12. Функции floor() и ceil()
Данная инструкция импортирования позволяет обращаться к членам модуля непосредственно, без указания имени модуля. Если бы мы импортировали модуль math иначе, то чтобы вызвать число л (пи), нам пришлось бы вводить math.pi. Точно так же для обращения к функциям floor () и ceil () пришлось бы использовать вызовы math.floor () и math.ceil (). Многие люди предпочитают не использовать инструкцию from x import *, так как это небезопасно. Дело в том, что имена в импортированном модуле могут конфликтовать с теми, которые программист определил в своей программе. Впрочем, вероятность появления таких конфликтов невелика. Кроме того, ничего страшного не произойдет, просто интерпретатор сообщит Вам об ошибке. С другой стороны, профессиональный программист никогда не станет импортировать модуль с помощью import *, если он недостаточно с ним знаком. Даже если ничего плохого не произойдет, это дурной тон программирования. Прежде чем что-либо импортировать, следует достать документацию на этот модуль и хорошо с ней познакомиться.
На рис. 3.12 показано практически все, что необходимо знать для правильного использования функций округления и преобразования типов. Только проверьте, чтобы количество открывающих круглых скобок соответствовало количеству закрывающих. И ещё на один момент хотелось бы обратить Ваше внимание. Посмотрите, как функция long() принимает в качестве аргумента другую функцию ceil (). Это важный момент, который необходимо хорошо запомнить: вместо чисел в качестве аргументов функций допускается использовать другие функции, которые обрабатывают свои аргументы.
Может возникнуть ещё один вопрос, связанный с округлением чисел с плавающей запятой, — как будут округляться отрицательные числа? Мы ненадолго отложим обсуждение этого вопроса и вернёмся к нему позже в этой главе.
Возведение в степень, как Вы должны помнить со школы, это, попросту говоря, умножение некоторого числа на себя опредёленное количество раз. Например, 22 означает умножить два на два, или возвести два в квадрат, что в результате даст 4. Точно так же 23 означает, что надо умножить два на два и на два, или возвести двойку в куб, что в результат даст 8.
*Прим. В. Шипкова: 2^2 или 2^3 - так вообще в программировании принято записывать степенные выражения. В Python принята несколько иная запись - 2**2=4, 2**3=9.
Экспоненциальное представление чисел, или, выражаясь более формально, форма записи чисел с плавающей запятой, использует показатель степени, чтобы при работе с очень большими числами избежать записи с многократным повторением нулей. Ранее, на рис. 3.6, был показан пример, в котором мы вычитали 10.0 - 9.99999 и получили неожиданный ответ: 9.99999999962е-006, тогда как предполагали увидеть 0.00001. Экспоненциальная форма записи содержит две части: показатель степени и дробную часть (которую иногда неправильно называют мантиссой). Что касается нашего удивительного ответа, то е-006 как раз и является показателем степени, а 9. 99999999962 — её дробная часть. Символ е как раз и указывает начало показателя степени (от английского exponent). Значение -006 — это фактическое значение показателя степени. Число, записанное подобным образом, обычно произносится как "9.99999999962 на 10 в минус шестой". Все очень просто, затруднение может состоять только в том, чтобы выговорить все эти девятки после десятичной запятой. Отрицательное значение показателя степени сообщает нам, что необходимо разделить единицу на значение нашего основания, т.е. на 10, опредёленное количество раз. К примеру, 10-1 является тем же самым, что и дробь 1/10 или 0,1. Показатель степени -6 в нашем примере означает разделить единицу на 10 шесть раз, или 1/1 000 000. Этой дроби соответствует число 0.000001. Чтобы убедиться в этом, посмотрите на рис. 3.13.
Рис. 3.13. Отрицательные показатели степени
Обратите внимание на последний результат, выведенный на экране, — число 0.000010. Это значение чрезвычайно близкое к тому, что мы ожидали увидеть с самого начала. Помните, что я говорил раньше о погрешностях округления при сложении и вычитании, которые имеют тенденцию существенно возрастать? Когда Вы оперируете с очень маленькими числами, порядка 10-6, эти ошибки суммируются и проявляют себя в значительной степени.
Экспоненциальное представление чисел весьма широко используется в программировании и научно-исследовательских работах. Поэтому имеет смысл познакомиться с этой формой записи поближе. Чаще всего Вам могли встречаться следующие значения: 103, т.е. 1000, 106, или миллион, 109 — миллиард и 1012 — триллион. (Интересно, что термины, применяемые к числам свыше миллиона, в разных странах могут иметь различные значения. Так, согласно американской терминологии, слово биллион (billion) обозначает миллиард.) А помните единицу, за которой следовала сотня нулей — гугол? Мы использовали это число в примерах несколько раньше. Так вот, для записи гугола в экспоненциальном представлении существуют два способа. Первый — в виде 10100, а второй — в виде 1010(?-что то не правильно указано) . Но в обоих случаях мы имеем одно и то же число. После того как Каснер ввёл в обиход термин гугол, другой математик предложил число под названием гуголплекс (googolplex), которое соответствует 10гугол. Боюсь, нам не хватит бумаги, чтобы записать это число в обычном виде. Информация для любознательных: на Web-странице этой книги можно найти программу на языке Python, которая выводит на печать числа гугол и гуголплекс. Она будет выполняться до тех пор, пока у Вас не лопнет терпение, или не исчерпается компьютерная память, или свободное пространство на жёстком диске компьютера, или пока Земля не упадет на Солнце (неизвестно, что произойдет первым). На рис. 3.14 показан быстрый метод вывода числа гугол в Python.
Рис. 3.14. Вывод числа гугол
Разобравшись с разными типами данных и форматами вывода числовых значений, перейдем на следующую ступеньку лестницы — написание математических формул. Безусловно, с математическими формулами Вы встречались не раз. Практически во всех этих формулах, за исключением самых элементарных, встречаются круглые скобки. Не правда ли, Вы это заметили? Круглые скобки присутствуют в формулах для того, чтобы указать порядок выполнения действий. Другими словами, взглянув на такую формулу, сразу видно, с чего именно необходимо начинать для её выполнения, даже если математическое действие в скобках Вам совершенно не знакомо и выглядит полной абракадаброй.
Python, как и все другие языки программирования, имеет сложную систему правил, называемых правилами приоритета операторов. С учётом этих правил опытный программист может управлять порядком выполнения математических формул без множества скобок. Это может повысить читабельность формул, если, конечно, соблюсти меру и следовать логике. Можно было бы и вообще обойтись без скобок. Для этого всего лишь необходимо запомнить каких-то 20—30 сложных правил, переписать свои математические выражения таким образом, чтобы они удовлетворяли этим правилам, но не соответствовали никакой человеческой логике, и тогда в Вашем коде не разберётся ни один шпион. Когда будете писать свои формулы, найдите золотую середину.
Как Вы поняли, лично я не большой поклонник следования правилам приоритета операторов. Я люблю, чтобы всё было, разложено по полочкам, причём как можно проще и явно. К тому же, я предпочитаю указывать компьютеру, что он должен для меня сделать, а не следовать его указаниям. Обобщая свой опыт работы, я установил свои собственные правила, которые, как мне кажется, намного проще.
Правило 1 Если в формуле используются только действия сложения или вычитания, забудьте вообще о круглых скобках.
Правило 2 Если операции сложения-вычитания перемежаются с умножением-делением, всегда используйте скобки.
Когда я делал только первые шаги в программировании, я несколько раз обжигался на правилах приоритета выполнения операторов, так как они не всегда следуют общепринятой логике. Скобки в этом плане более надёжны, так как обладают абсолютным приоритетом. Рассмотрим применение скобок на простом примере, показанном на рис. 3.15. Если нам нужно найти отношение суммы на число, то следующее выражение будет неправильным: 400 + 1 / 3. Чтобы исправить ситуацию, заключите сумму 400 + 1 в скобки.
Рис. 3.15. Пример использования скобок
Если ваша формула слишком длинная, то хоть используйте скобки, хоть не используйте, читабельной она никогда не станет. Попробуйте разбить формулу на несколько строк. Это улучшит её читабельность, что Вы прочувствуете во время отладки программы. Помните также о том, что когда-нибудь с вашим кодом может работать кто-то другой. Не доводите Вашего коллегу до психоза, тем более что вернувшись к своей собственной программе через пару месяцев, Вы сами окажетесь не в лучшем положении. Поэтому критическим взглядом пройдитесь по каждой строке кода и спросите себя: "Смогу ли я вспомнить через шесть недель, что выполняет данная строка?" Если возникают сомнения, то формулу лучше переписать прямо сейчас.
Одной из особенностей Python, которую необходимо учитывать при обработке чисел любого типа, является механизм выполнения функций floor () и ceil () для отрицательных аргументов. По выполнению этих функций Python отличается от языков С и C++, поэтому если Вы работали с любым из этих языков, то должны быть начеку, чтобы предупредить появление ошибок. Данная проблема проиллюстрирована на рис. 3.16.
Рис. 3.16. Округление отрицательных чисел
В языке С применение функции floor() к аргументу pi даёт результат 3, но если применить её к значению -pi, то получим —3, а в Python — —4. Если же используется функция ceil(), то получится -4 и —3 соответственно. Почему так происходит? По определению, в обоих языках функция floor() осуществляет "округление вниз". Почему же тогда получаются разные результаты? Дело в том, что эти языки по-разному понимают, что такое "округление вниз". В случае с Python слово вниз подразумевает меньше, аналогично тому, как 0,0001<0<10000 и число 0.0000000000001 меньше числа 0.0001. Тогда как в С меньше означает ближе к нулю. Таким образом, в Python число —4 "лежит ниже", чем —3.14159265359. При целочисленном делении результат получается таким же, как при применении функции floor (). Результат округляется к меньшему числу, а не к тому, которое находится ближе к нулю.
Эти несостыковки в логике языков могут привести к неожиданным проблемам. Например, работая в С, я написал функцию, которая вычисляла разницу в днях между григорианским и юлианским календарями. Эта разница носит название отклонение и является константой в промежутке от 100 до 200 лет. Я перенес эту функцию в Python и быстренько проверил её работоспособность. Казалось, что все работает нормально. Но через два-три дня после этого мне подвернулся случай опробовать её на отрицательных датах. Результаты её работы утверждали, что до 0-го года не было никаких отклонений. (В этой программе годы до нашей эры выражались отрицательными цифрами.) Это была явная ошибка. Я исследовал код функции и вышел на строку, которая содержала следующее выражение: devn = 2 - leaper + -(leaper/4). В этом выражении devn и leaper являются переменными, назначение которых состоит в сохранении значений. (С переменными Вы познакомитесь в следующей главе.) Переменная leaper содержит значение столетия. Если это значение выражалось отрицательной величиной, то результат отношения leaper/4 округлялся до меньшего значения, а не до того, которое ближе к нулю. Поэтому программа работала в С, но допускала ошибки в Python.
В целом вычисления с датами в Python выполнять даже удобнее, чем в других языках. Новичкам будет проще. Они воспримут это как должное, так как на них не давит груз знаний о том, как работают аналогичные функции в других языках. Я же знал, как должна была выполняться эта функция, и был просто обескуражен, когда она не работала ожидаемым образом. Моя ошибка состояла в том, что я перенес код с языка С на Python, не проверив должным образом, насколько их функции соответствуют друг другу.
Если у Вас богатый опыт программирования, заставьте себя внимательно изучить средства Python, вчитываясь во все детали, чтобы не допускать подобные оплошности.
Полезное свойство Python, которое лично мне очень понравилось, — встроенная поддержка длинных целых чисел. Я был разочарован, работая в С и C++ над календарем Майя. Эти языки строго отслеживают тип данных, и чтобы иметь возможность обрабатывать в программе как обычные, так длинные целые числа, приходилось дважды переписывать код для обоих типов. Для Python достаточно явно указать длинное число и для обработки его использовать те же функции, что и для обычного числа. Конечно, Python стал бы ещё удобнее, если бы вообще не видел разницы между обычными и длинными числами. Действительно, различие между этими типами чисел совершенно условно и связано только с объёмом памяти, предоставляемым для сохранения значения. Гуидо обещал в скором будущем сделать прозрачным переход от типа к типу. А пока Вам придётся проявлять внимательность с арифметическими операциями, при выполнении которых возможно переполнение целых 32-битовых знаковых чисел. Если Вам, к примеру, случится столкнуться с календарем народов Майя, то Вы не успеете и глазом моргнуть, как преодолеете двухмиллиардный (плюс мелочь) предел.
Существуют встроенные методы автоматического преобразования всех целых чисел в программе в длинные целые, но мы не будем сейчас останавливаться на них. Можно также вручную помечать все значения в программе как длинные. Но за подобное упрощение придётся расплачиваться понижением быстродействия. Впрочем, для большинства программ прекрасно подходят обычные 32-разрядные целые числа.
В этой главе мы рассмотрели все основные арифметические операторы языка Python и опробовали их с помощью интерпретатора. Вы должны были ощутить атмосферу работы с Python и привыкнуть к окну IDLE. Надеюсь, что в следующей главе, когда мы начнём обсуждать переменные и вопросы управления потоками данных, Вы будете довольно комфортно чувствовать себя. Вы также узнали, как выполняется округление чисел, каковы особенности обработки чисел с плавающей запятой, что такое экспоненциальное представление чисел, зачем применяются скобки. Кроме того, теперь Вы знаете, что логика Python несколько отличается от логики других языков программирования.
Для обобщения материала посмотрите табл. 3.1, в которой представлены все математические операторы, используемые в Python. Некоторые из этих операторов будут подразумевать совершенно иное действие, когда будут применяться к объектам, не являющимся числами. Мы будем подробно рассматривать особенности применения этих операторов по мере освоения нового материала.
Таблица 3.1. Математические операторы в Python
Символ
Значение
1 +
Сложение/тождество
2 -
Вычитание/отрицание
3 *
Умножение
4 /
Деление
5 %
Деление по модулю
6 **
Возведение в степень
7 divmod (x,у)
Функция, возвращающая значения х/у и х%у
Что лучше, компьютер или счеты?
Дело вкуса, привычек и цели применения. Счетами проще отбиваться от грабителя, пытающегося залезть в Вашу кассу.
Когда было изобретено экспоненциальное представление чисел?
Два первых случая использования такого представления чисел были зафиксированы незадолго до 1890 года, если только это не более позднее добавление переводчиков. По-настоящему первое указание на эту форму записи было зафиксировано в журнале Jean's Theoretical Mechanics ("Теоретическая механика") за 1907 г., где масса Земли приводится в виде 6х1027 г. За эту цитату мы должны быть благодарны Джону Харперу (John Harper) из университета Виктория, Веллингтон, Новая Зеландия (Victoria University, Wellington).
Как можно сообщить интерпретатору Python, что некоторое число имеет формат длинного целого числа?
а) long("10000000000000000000000000000000000000")
б) 100000000000000000000000000000000L
в) string.atol("100000000000000000000000000000")
г) любое целое число/1L
Что произойдет, если умножить число с плавающей запятой на длинное целое число?
а) Вы получите сообщение об ошибке OverflowError.
б) Python преобразует результат в комплексное число.
в) Python сообщит Вам, что в любом случае Вам не понять ответ.
г) Когда длинное целое число состоит примерно из 300 (или более) цифр, Python вместо числового ответа посылает строку 1.#INF (или inf — для Linux). В остальных случаях он выдает ответ, используя экспоненциальное представление.
Если двоичное число по основанию 2, а шестнадцатеричное по основанию 16, то что такое восьмеричное число и где оно используется?
а) Числа с основанием 32; используются программистами Macintosh.
б) Это понятие не имеет никакого отношения к числам; термин восьмеричное (octal) — это название символа #.
в) Числа с основанием 8; используются программистами UNIX.
г) Числа с основанием 8; но никто их не использует.
Можно использовать все указанные методы.
г. Для чисел с плавающей запятой в Windows и Linux максимальным установлено значение с показателем степени ±308. Это достаточно большое (или достаточно маленькое) число. При выходе за эти пределы библиотеки, поддерживающие вычисления с плавающей запятой, возвращают стандартный символ бесконечности.
в. Восьмеричное число — конечно же, это число с основанием 8. И числа в таком формате действительно главным образом используют программисты, разрабатывающие приложения для UNIX. Наиболее наглядным примером применения таких чисел является программа chmod для UNIX, которая позволяет изменять права доступа к файлам. А символ #, действительно, имеет необычное название — октоторп (octothorpe).
Если Вас беспокоит проблема потери точности вычислений с использованием чисел с плавающей запятой, познакомьтесь с книгой Дональда Кнута, "Искусство программирования".
Если Вас заинтересовала тема больших чисел, таких как гугол, ниже приводится перечень нескольких Web-страниц, которые настоятельно рекомендуется исследовать. Некоторые из приведенных там алгоритмов поддаются воплощению на языке Python.
- Большие конечные и бесконечные числа: http://www.sci.wsu.edu/math/faculty/hudelson/mose.r.html
- Познакомьтесь с числом газиллион (gazillion): http://www.straightdope.com/mailbag/mgazilli.html
- Как получить число гуголплекс: http://WWW/~fp/Tools/GetAGoogol.html
- Названия чисел разного порядка (от маленьких до больших): http://studwww.rug.ас.be/~hvernaev/FAQ/node2 6.html
- И снова число гуголплекс: http://www/~fp/Topls/Googool.html (лучший узел, касающийся этого вопроса)
- Число pi и его друзья: http://www.go2net.com/internet/useless/useless/pi.html
- Эпоха расцвета индейцев Майя и эпоха глифов: http://www.pauahtun.org/calglypn.html
Попробуйте выяснить, насколько большим должно быть число, чтобы вызвать сбой в работе Python или "подвесить" Ваш компьютер? (Только сначала сделайте резервные копии всех файлов.)